KV Cache Invalidation
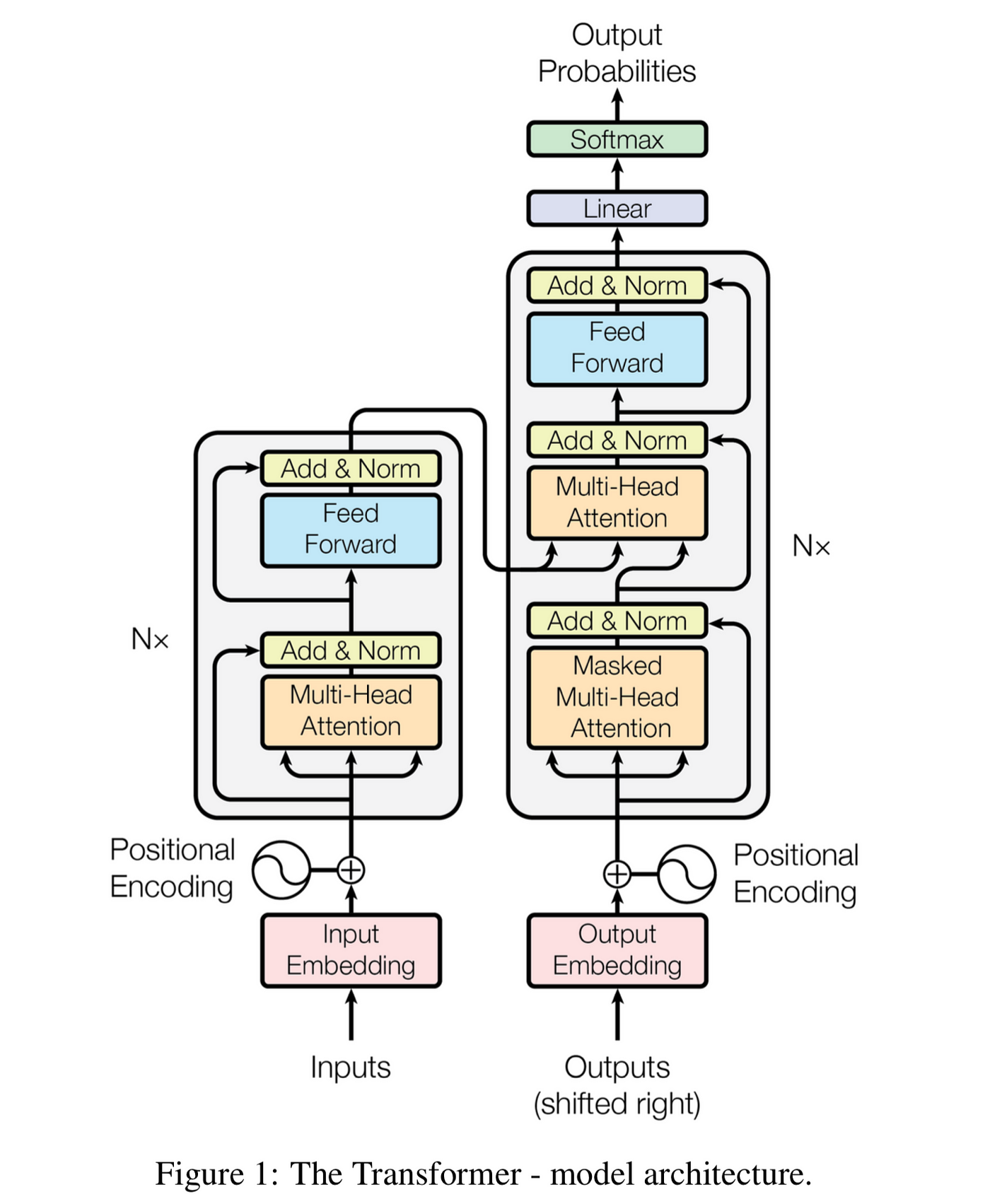
Why removing context from an LLM conversation forces full recomputation Over the holiday break, I had a conversation with a friend about prompt caching. Everyone's intuition about context engineering is sensible: if you're chatting with ChatGPT or Claude and the conversation accumulates irrelevant context, removing it should help the model focus. Better accuracy, right? Yes, but there's a catch. Removing tokens from the middle of a conversation invalidates the KV cache—a key mechanism that speeds up LLM inference. You don't just lose a bit of cached work; you lose everything after the edit. This is why claude.ai, ChatGPT, or Claude Code don't frequently edit or delete earlier messages1. As a Claude Code PM put it: "Coding agents would be cost prohibitive if they didn't maintain the prompt cache between turns." This post explains why. Compaction does happen, but infrequently. LLMs generate text one token at a time. Given a sequence of tokens $t_1, \ldots, t_i$, the model predicts a probability distribution over the next token: $$P(t_{i+1} | t_1, \ldots, t_i)$$ To generate a response, the model samples from this distribution (likely Paris in the figure above), appends the new token to the context, and repeats. Each new token requires a forward pass through the entire model, processing the full context. Modern LLMs use the transformer architecture. Here's the famous diagram from "Attention Is All You Need": The grey box marked "Nx" to the right is a decoder block—it's repeated $L$ times. Each block contains a masked multi-head attention and a feed-forward network.2 Each token $t_i$ starts as an embedding vector $x_i$. As it passes through the blocks, this vector gets transformed. Call the vector for position $i$ after block $\ell$ the hidden state $z_i^{(\ell)}$. Each block feeds into the next: $z_i^{(\ell)}$ becomes the input for computing $z_i^{(\ell+1)}$. After $L$ blocks, the final hidden state $z_i^{(L)}$ is used to predict $P(t_{i+1} | t_1, \ldots, t_i)$, that is, the probability distribution we started with. The diagram shows the original encoder-decoder architecture. Modern LLMs like GPT and Claude are decoder-only: they omit the left side (encoder) and the middle "Multi-Head Attention" that attends to encoder outputs. The masked multi-head attention in each block computes three vectors from each hidden state $z_i^{(\ell)}$—for every position $i$, every block $\ell$, and every attention head $h$ (Llama 3.1 405B has 126 blocks and 128 heads): Position $i$ attends to all positions $j \leq i$ by comparing its query against their keys, then taking a weighted sum of their values. This means $z_i^{(\ell)}$, and Q, K, V, depend on all preceding tokens, not just $t_i$ alone. The KV cache exploits a key observation: when generating new tokens, the K and V vectors for previous positions don't change. So we cache them. For each new token, we compute its Q, K, V, then reuse the cached K's and V's for attention. This turns $O(n^2)$ per-token work into $O(n)$. Now consider removing a token from position $j$. What happens to the cached K and V vectors? Remove token $j$, and every hidden state $z_{j+1}^{(\ell)}, z_{j+2}^{(\ell)}, \ldots$ changes—they all attended to position $j$ but no longer do. Per previous section, changed hidden states mean changed K and V vectors. The entire cache from position $j$ onward is now stale. Prompt caching requires exact prefix match. API providers like Anthropic and OpenAI cache the KV state for prompts. If your new request shares an exact prefix with a previous one, they can reuse the cache. But if you modify anything—even a single token in the middle—the cache is useless from that point onward. Cache invalidation is expensive. Consider editing a token early in a 50,000-token conversation. Every position after the edit needs its K and V vectors recomputed—across all blocks and heads. That's over 800 million vector computations for Llama 3.1 405B. Anthropic's prompt caching prices cache hits at 10% of base input token cost; a cache miss means paying the full price. Latency suffers too: cache hits can reduce time-to-first-token by up to 85% for long prompts. You can append, but you can't edit. Adding tokens to the end is cheap: just extend the cache. Inserting or deleting in the middle forces recomputation of everything downstream. This is why conversation history in chatbots tends to grow monotonically. The accuracy-cost tradeoff is real. Removing irrelevant context might improve model focus, but you pay with compute. For long conversations, this cost can be substantial. Sometimes it's worth it; often it's not. One approach: Letta suggests prompt edits asynchronously during idle periods ("via sleep-time agents"), so the cache reconstruction happens when the user isn't waiting. The notation here matches what's used above. $$x_i = E[t_i] + p_i, \quad E \in \mathbb{R}^{V \times d}, \quad p_i \in \mathbb{R}^d$$ where $t_i$ is the token index and $p_i$ is the positional encoding. Let $X^{(0)} = [x_1, \dots, x_n] \in \mathbb{R}^{d \times n}$ be the initial input to the transformer blocks. For block $\ell = 1, \dots, L$, with input $X^{(\ell-1)} \in \mathbb{R}^{d \times n}$: Multi-Head Masked Attention Queries, keys, and values for head $h$: $$Q^{(h)}(x_i) = (W_h^{Q})^T x_i, \quad K^{(h)}(x_i) = (W_h^{K})^T x_i, \quad V^{(h)}(x_i) = (W_h^{V})^T x_i$$ where $W_h^{Q}, W_h^{K}, W_h^{V} \in \mathbb{R}^{d \times k}$. Masked Attention Weights $$\alpha_{i,j}^{(h)} = softmax_j \left(\frac{Q^{(h)}(x_i) \cdot K^{(h)}(x_j)}{\sqrt{k}} + M_{i,j}\right)$$ where the causal mask $M_{i,j} = 0$ if $j \leq i$, and $M_{i,j} = -\infty$ if $j > i$. Output for Each Head $$u_i^{(h)} = \sum_{j=1}^{i} \alpha_{i,j}^{(h)} V^{(h)}(x_j) \in \mathbb{R}^{k}$$ Concatenated Output $$u_i' = \sum_{h=1}^{H} (W_h^{O})^T u_i^{(h)}, \quad W_h^{O} \in \mathbb{R}^{k \times d}$$ Residual + LayerNorm $$u_i = \text{LayerNorm}(x_i + u_i'; \gamma_1, \beta_1)$$ For each position $i$: $$z_i' = (W_2)^T \text{ReLU}((W_1)^T u_i), \quad W_1 \in \mathbb{R}^{d \times m}, , W_2 \in \mathbb{R}^{m \times d}$$ Residual + LayerNorm (Block Output) $$z_i = \text{LayerNorm}(u_i + z_i'; \gamma_2, \beta_2)$$ Let $X^{(\ell)} = [z_1, \dots, z_n]$. This becomes the input to block $\ell + 1$. After $L$ blocks, let $Z = X^{(L)}$ be the final representations. $$\text{logits}_i = E z_i + b, \quad E \in \mathbb{R}^{V \times d}, , b \in \mathbb{R}^V$$ where $E$ is often tied with input embeddings. Prediction Probabilities $$P(t_{i+1} | t_1, \dots, t_i) = \text{softmax}(\text{logits}_i)$$ The output at position $i$ predicts the next token $t_{i+1}$, using only information from tokens $t_1, \dots, t_i$ due to causal masking. References: This post was written in collaboration with Claude (Opus 4.5).
Next-Token Prediction
The Transformer Forward Pass
The KV Cache
Why Removing Tokens Breaks the Cache
Implications
Appendix: Transformer Math
Full derivation
Notation
Step 1: Input Token Embeddings
Steps 2-6: Decoder Block (repeated L times)
Steps 7-8: Feed-Forward Network
Steps 9-10: Output Logits and Probabilities