From Keys to Protocols: ECDH and ECDSA (Part 2/2)
How elliptic curve math enables secure key exchange and digital signatures In Part 1, we built up the machinery: fields, groups, elliptic curves, and the discrete logarithm problem (DLP). We ended with a key pair: pick a secret integer (I called it $n$ there; I'll use $d$ here to match standard cryptographic notation), then compute: $$Q = dG$$ $Q$ is the public key and $d$ is the private key. The forward direction is fast, but recovering $d$ from $Q$ means solving the DLP, which is infeasible. This post shows how that asymmetry enables two protocols solving different problems: ECDH for establishing shared keys, and ECDSA for digital signatures. Alice wants to send Bob a secret message. Encryption scrambles the message into ciphertext; decryption reverses the process. Symmetric encryption uses one key for both operations. It's fast, but it has a bootstrap problem: how does Alice send Bob that key? If she sends it over the same channel as the message, an eavesdropper intercepts both. She needs a secure channel to send the key, but that's exactly what she's trying to create. Chicken and egg. Asymmetric encryption could solve this: anyone can encrypt with Bob's public key, but only Bob's private key can decrypt. No secret travels over the wire. The cost? Asymmetric operations involve expensive math (point multiplications, modular exponentiations), while symmetric ciphers use simple bitwise operations. The difference in complexity is roughly 1000x. The solution is a hybrid approach: use asymmetric cryptography once to establish a shared key, then switch to symmetric for the actual messages. This is exactly what ECDH does. Elliptic Curve Diffie-Hellman lets two parties derive a shared key over a public channel: Both arrive at the same point $S$ without ever transmitting $a$ or $b$. Why does this work? Because $a(bG) = (ab)G = b(aG)$: the commutativity comes from integer multiplication, not any special property of the curve. Why is this secure? An eavesdropper sees $A$, $B$, and $G$, but computing $abG$ from these requires solving the DLP to recover $a$ or $b$. That's the hard direction we established in Part 1. What happens next: Alice and Bob hash the x-coordinate of $S$ to derive a symmetric key, then use it with a symmetric cipher like AES (the standard for same-key encryption). ECDH doesn't encrypt anything itself; it bootstraps the shared key that makes symmetric encryption possible.1 If you've used PGP or GPG with a modern key, you've used this. The hybrid structure is the same: ECDH establishes the session key, AES encrypts the message. This works elegantly for two parties. Group chats are harder: the naive approach requires $\binom{N}{2} = \frac{N(N-1)}{2}$ pairwise key exchanges for $N$ participants. Real messaging apps use more sophisticated protocols to avoid this quadratic scaling. ECDH solves secrecy. ECDSA (Elliptic Curve Digital Signature Algorithm) solves a different problem: authenticity. Consider Ethereum transactions. They're broadcast publicly; secrecy isn't the goal. The network needs to verify that the account holder actually authorized the transaction. A digital signature proves you know the private key $d$ without revealing it, and binds that proof to a specific message. To sign a message $m$ with private key $d$: $$s = k^{-1}(z + rd) \mod n$$ The signature is the pair $(r, s)$. Given a message $m$, signature $(r, s)$, and public key $Q$: The verifier reconstructs $R$ without knowing $k$ or $d$. Here's the algebra: $$P = u_1 G + u_2 Q = zs^{-1}G + rs^{-1}Q$$ Since $Q = dG$: $$P = zs^{-1}G + rs^{-1}dG = s^{-1}(z + rd)G$$ From the signing equation, $s = k^{-1}(z + rd)$, so $s^{-1} = k/(z + rd)$. Substituting: $$P = \frac{k}{z + rd}(z + rd)G = kG = R$$ The x-coordinate of $P$ equals $r$ precisely when the signer knew $d$. The random value $k$ must be truly random and never reused. If the same $k$ signs two different messages, an attacker can algebraically recover your private key $d$. This isn't theoretical: Sony's PlayStation 3 code signing was broken in 2010 because they used a constant $k$, allowing attackers to extract the private key and sign arbitrary code. One elliptic curve, one hard problem, two protocols. ECDH gives you secrecy: two parties derive a shared key over a public channel, then use it for symmetric encryption. ECDSA gives you authenticity: prove you authorized something without revealing your private key. This shows how the abstract group theory from Part 1 isn't just elegant mathematics. It's the foundation securing your encrypted messages, your cryptocurrency transactions, and much of the internet's infrastructure. This post was written in collaboration with Claude (Opus 4.5).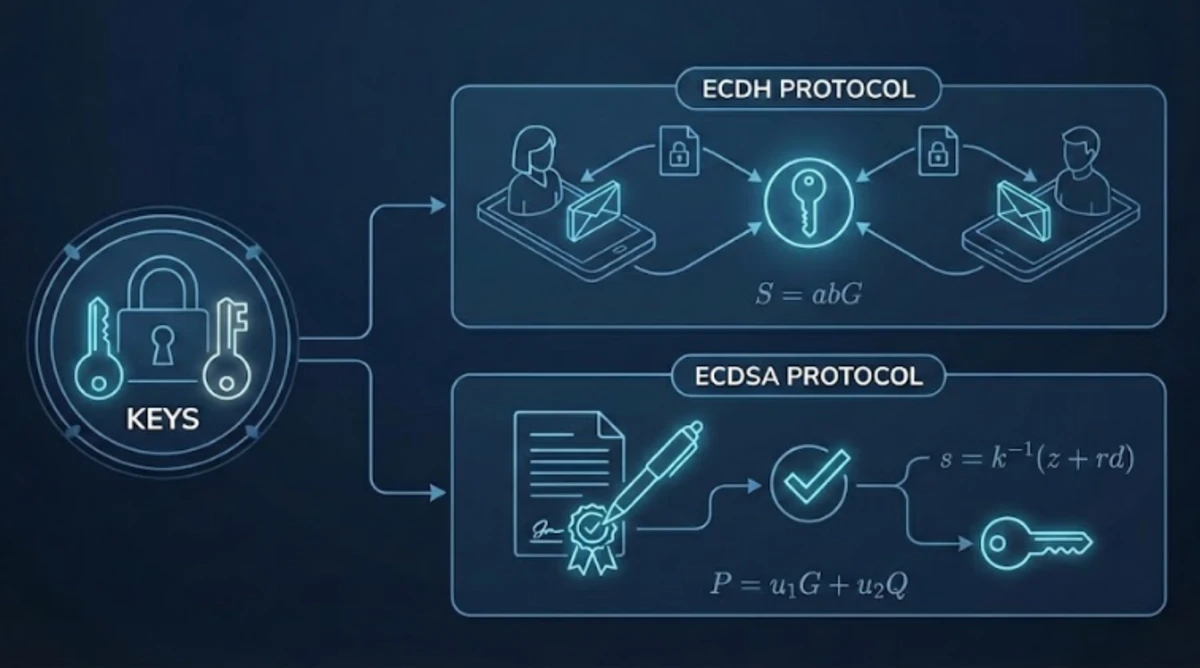
ECDH: Shared Keys
The Problem
The Protocol
ECDSA: Digital Signatures
Signing
Verification
Why Verification Works
The Nonce
Takeaway