Invalidation du cache KV
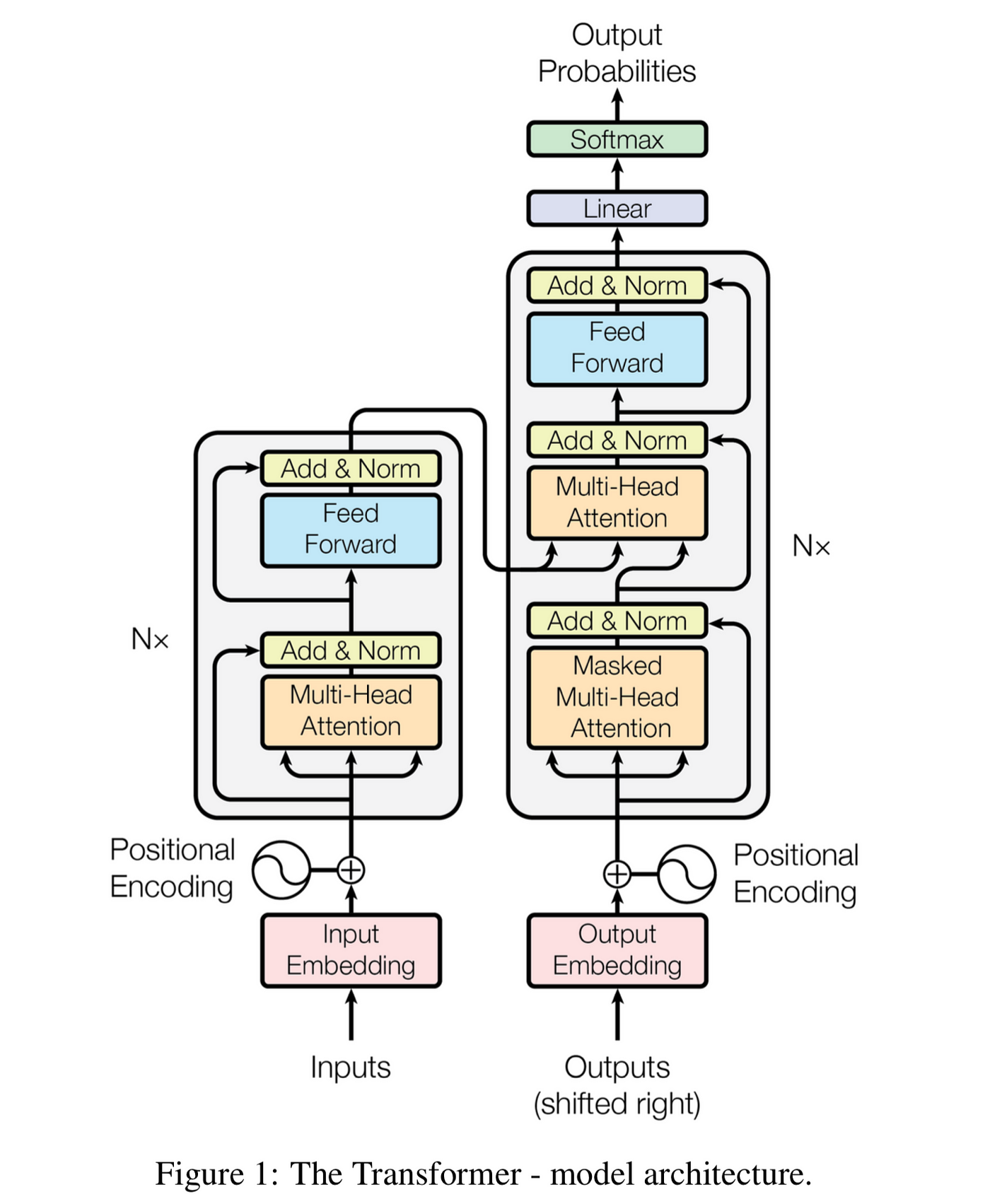
Pourquoi supprimer du contexte d'une conversation LLM force un recalcul complet Pendant les fêtes, j'ai eu une conversation avec un ami à propos de la mise en cache des prompts. L'intuition de chacun sur l'ingénierie de contexte est logique : si vous discutez avec ChatGPT ou Claude et que la conversation accumule du contexte non pertinent, le supprimer devrait aider le modèle à se concentrer. Meilleure précision, non ? Oui, mais il y a un piège. Supprimer des tokens au milieu d'une conversation invalide le cache KV — un mécanisme clé qui accélère l'inférence des LLM. On ne perd pas juste un peu de calcul mis en cache ; on perd tout ce qui suit la modification. C'est pourquoi claude.ai, ChatGPT ou Claude Code ne modifient ou ne suppriment pas fréquemment les messages précédents1. Comme l'a exprimé un PM de Claude Code sur Twitter : « Les agents de programmation seraient d'un coût prohibitif s'ils ne maintenaient pas le cache de prompt entre les tours. » Ce billet explique pourquoi. La compaction se produit, mais rarement. Les LLM génèrent du texte un token à la fois. Étant donné une séquence de tokens $t_1, \ldots, t_i$, le modèle prédit une distribution de probabilité sur le prochain token : $$P(t_{i+1} | t_1, \ldots, t_i)$$ Pour générer une réponse, le modèle échantillonne cette distribution (probablement Paris dans la figure ci-dessus), ajoute le nouveau token au contexte, et répète. Chaque nouveau token nécessite une passe forward à travers tout le modèle, traitant le contexte complet. Les LLM modernes utilisent l'architecture Transformer. Voici le fameux diagramme de « Attention Is All You Need » : La boîte grise marquée « Nx » à droite est un bloc décodeur — il est répété $L$ fois. Chaque bloc contient une attention multi-têtes masquée et un réseau feed-forward.2 Chaque token $t_i$ commence comme un vecteur d'embedding $x_i$. En traversant les blocs, ce vecteur se transforme. Appelons le vecteur pour la position $i$ après le bloc $\ell$ l'état caché $z_i^{(\ell)}$. Chaque bloc alimente le suivant : $z_i^{(\ell)}$ devient l'entrée pour calculer $z_i^{(\ell+1)}$. Après $L$ blocs, l'état caché final $z_i^{(L)}$ sert à prédire $P(t_{i+1} | t_1, \ldots, t_i)$, c'est-à-dire la distribution de probabilité du début. Le diagramme montre l'architecture encodeur-décodeur originale. Les LLM modernes comme GPT et Claude sont décodeur uniquement : ils omettent le côté gauche (encodeur) et la « Multi-Head Attention » du milieu qui prête attention aux sorties de l'encodeur. L'attention multi-têtes masquée dans chaque bloc calcule trois vecteurs à partir de chaque état caché $z_i^{(\ell)}$ — pour chaque position $i$, chaque bloc $\ell$, et chaque tête d'attention $h$ (Llama 3.1 405B a 126 blocs et 128 têtes) : La position $i$ prête attention à toutes les positions $j \leq i$ en comparant sa query à leurs keys, puis en prenant une somme pondérée de leurs values. Cela signifie que $z_i^{(\ell)}$, ainsi que Q, K, V, dépendent de tous les tokens précédents, pas seulement de $t_i$ seul. Le cache KV exploite une observation clé : lors de la génération de nouveaux tokens, les vecteurs K et V des positions précédentes ne changent pas. On les met donc en cache. Pour chaque nouveau token, on calcule ses Q, K, V, puis on réutilise les K et V en cache pour l'attention. Cela transforme un travail $O(n^2)$ par token en $O(n)$. Considérons maintenant la suppression d'un token à la position $j$. Que se passe-t-il pour les vecteurs K et V en cache ? Supprimez le token $j$, et chaque état caché $z_{j+1}^{(\ell)}, z_{j+2}^{(\ell)}, \ldots$ change — ils prêtaient tous attention à la position $j$, mais ce n'est plus le cas. Selon la section précédente, des états cachés modifiés signifient des vecteurs K et V modifiés. Tout le cache à partir de la position $j$ est désormais obsolète. La mise en cache des prompts nécessite une correspondance exacte du préfixe. Les fournisseurs d'API comme Anthropic et OpenAI mettent en cache l'état KV des prompts. Si votre nouvelle requête partage un préfixe exact avec une précédente, ils peuvent réutiliser le cache. Mais si vous modifiez quoi que ce soit — même un seul token au milieu — le cache est inutilisable à partir de ce point. L'invalidation du cache coûte cher. Imaginez modifier un token au début d'une conversation de 50 000 tokens. Chaque position après la modification doit voir ses vecteurs K et V recalculés — à travers tous les blocs et toutes les têtes. Cela représente plus de 800 millions de calculs de vecteurs pour Llama 3.1 405B. Le prompt caching d'Anthropic facture les succès de cache à 10 % du coût de base des tokens d'entrée ; un échec de cache signifie payer le plein tarif. La latence en souffre aussi : les succès de cache peuvent réduire le temps jusqu'au premier token de jusqu'à 85 % pour les prompts longs. On peut ajouter, mais pas modifier. Ajouter des tokens à la fin est peu coûteux : on étend simplement le cache. Insérer ou supprimer au milieu force le recalcul de tout ce qui suit. C'est pourquoi l'historique des conversations dans les chatbots tend à croître de façon monotone. Le compromis précision-coût est réel. Supprimer du contexte non pertinent peut améliorer la concentration du modèle, mais on paie en calcul. Pour les longues conversations, ce coût peut être substantiel. Parfois ça en vaut la peine ; souvent non. Une approche : Letta suggère de modifier les prompts de façon asynchrone pendant les périodes d'inactivité (via des « sleep-time agents »), pour que la reconstruction du cache se fasse quand l'utilisateur n'attend pas. La notation ici correspond à celle utilisée ci-dessus. $$x_i = E[t_i] + p_i, \quad E \in \mathbb{R}^{V \times d}, \quad p_i \in \mathbb{R}^d$$ où $t_i$ est l'indice du token et $p_i$ est l'encodage positionnel. Soit $X^{(0)} = [x_1, \dots, x_n] \in \mathbb{R}^{d \times n}$ l'entrée initiale des blocs transformer. Pour le bloc $\ell = 1, \dots, L$, avec entrée $X^{(\ell-1)} \in \mathbb{R}^{d \times n}$ : Attention multi-têtes masquée Queries, keys et values pour la tête $h$ : $$Q^{(h)}(x_i) = (W_h^{Q})^T x_i, \quad K^{(h)}(x_i) = (W_h^{K})^T x_i, \quad V^{(h)}(x_i) = (W_h^{V})^T x_i$$ où $W_h^{Q}, W_h^{K}, W_h^{V} \in \mathbb{R}^{d \times k}$. Poids d'attention masqués $$\alpha_{i,j}^{(h)} = softmax_j \left(\frac{Q^{(h)}(x_i) \cdot K^{(h)}(x_j)}{\sqrt{k}} + M_{i,j}\right)$$ où le masque causal $M_{i,j} = 0$ si $j \leq i$, et $M_{i,j} = -\infty$ si $j > i$. Sortie pour chaque tête $$u_i^{(h)} = \sum_{j=1}^{i} \alpha_{i,j}^{(h)} V^{(h)}(x_j) \in \mathbb{R}^{k}$$ Sortie concaténée $$u_i' = \sum_{h=1}^{H} (W_h^{O})^T u_i^{(h)}, \quad W_h^{O} \in \mathbb{R}^{k \times d}$$ Résidu + LayerNorm $$u_i = \text{LayerNorm}(x_i + u_i'; \gamma_1, \beta_1)$$ Pour chaque position $i$ : $$z_i' = (W_2)^T \text{ReLU}((W_1)^T u_i), \quad W_1 \in \mathbb{R}^{d \times m}, , W_2 \in \mathbb{R}^{m \times d}$$ Résidu + LayerNorm (sortie du bloc) $$z_i = \text{LayerNorm}(u_i + z_i'; \gamma_2, \beta_2)$$ Soit $X^{(\ell)} = [z_1, \dots, z_n]$. Ceci devient l'entrée du bloc $\ell + 1$. Après $L$ blocs, soit $Z = X^{(L)}$ les représentations finales. $$\text{logits}_i = E z_i + b, \quad E \in \mathbb{R}^{V \times d}, , b \in \mathbb{R}^V$$ où $E$ est souvent lié aux embeddings d'entrée. Probabilités de prédiction $$P(t_{i+1} | t_1, \dots, t_i) = \text{softmax}(\text{logits}_i)$$ La sortie à la position $i$ prédit le prochain token $t_{i+1}$, en utilisant uniquement l'information des tokens $t_1, \dots, t_i$ grâce au masquage causal. Références : Ce billet a été écrit en collaboration avec Claude (Opus 4.5).
Prédiction du prochain token
La passe forward du Transformer
Le cache KV
Pourquoi supprimer des tokens casse le cache
Implications
Annexe : Mathématiques du Transformer
Dérivation complète
Notation
Étape 1 : Embeddings des tokens d'entrée
Étapes 2-6 : Bloc décodeur (répété L fois)
Étapes 7-8 : Réseau feed-forward
Étapes 9-10 : Logits et probabilités de sortie