Des clés aux protocoles : ECDH et ECDSA (Partie 2/2)
Comment les mathématiques des courbes elliptiques permettent l'échange de clés sécurisé et les signatures numériques Dans la 1re partie, nous avons construit la machinerie : corps, groupes, courbes elliptiques et le problème du logarithme discret (DLP). Nous avons terminé avec une paire de clés : choisir un entier secret (je l'avais appelé $n$ ; j'utiliserai $d$ ici pour suivre la notation standard en cryptographie), puis calculer : $$Q = dG$$ $Q$ est la clé publique et $d$ est la clé privée. Le calcul direct est rapide, mais retrouver $d$ à partir de $Q$ revient à résoudre le DLP, ce qui est infaisable. Cet article montre comment cette asymétrie permet deux protocoles résolvant des problèmes différents : ECDH pour établir des clés partagées, et ECDSA pour les signatures numériques. Alice veut envoyer un message secret à Bob. Le chiffrement brouille le message en texte chiffré ; le déchiffrement inverse le processus. Le chiffrement symétrique utilise une seule clé pour les deux opérations. C'est rapide, mais il y a un problème d'amorçage : comment Alice envoie-t-elle cette clé à Bob ? Si elle l'envoie par le même canal que le message, un espion intercepte les deux. Elle a besoin d'un canal sécurisé pour envoyer la clé, mais c'est exactement ce qu'elle essaie de créer. L'œuf ou la poule. Le chiffrement asymétrique pourrait résoudre cela : n'importe qui peut chiffrer avec la clé publique de Bob, mais seule la clé privée de Bob peut déchiffrer. Aucun secret ne circule sur le réseau. Le coût ? Les opérations asymétriques impliquent des mathématiques coûteuses (multiplications de points, exponentiations modulaires), tandis que les chiffrements symétriques utilisent de simples opérations bit à bit. La différence de complexité est d'environ 1000x. La solution est une approche hybride : utiliser la cryptographie asymétrique une fois pour établir une clé partagée, puis passer au symétrique pour les messages eux-mêmes. C'est exactement ce que fait ECDH. Elliptic Curve Diffie-Hellman permet à deux parties de dériver une clé partagée sur un canal public : Les deux arrivent au même point $S$ sans jamais transmettre $a$ ou $b$. Pourquoi ça marche ? Parce que $a(bG) = (ab)G = b(aG)$ : la commutativité vient de la multiplication des entiers, pas d'une propriété spéciale de la courbe. Pourquoi est-ce sécurisé ? Un espion voit $A$, $B$ et $G$, mais calculer $abG$ à partir de ceux-ci nécessite de résoudre le DLP pour retrouver $a$ ou $b$. C'est le sens difficile que nous avons établi dans la 1re partie. Ensuite : Alice et Bob hachent la coordonnée x de $S$ pour dériver une clé symétrique, puis l'utilisent avec un algorithme comme AES (le standard du chiffrement symétrique). ECDH ne chiffre rien lui-même ; il amorce la clé partagée qui rend le chiffrement symétrique possible.1 Si vous avez utilisé PGP ou GPG avec une clé moderne, vous avez utilisé cela. La structure hybride est la même : ECDH établit la clé de session, AES chiffre le message. Cela fonctionne bien pour deux parties. Les conversations de groupe sont plus complexes : l'approche naïve nécessite $\binom{N}{2} = \frac{N(N-1)}{2}$ échanges de clés pour $N$ participants. Les vraies applications de messagerie utilisent des protocoles plus sophistiqués pour éviter cette croissance quadratique. ECDH assure la confidentialité. ECDSA (Elliptic Curve Digital Signature Algorithm) s'attaque à un problème différent : l'authenticité. Considérons les transactions Ethereum. Elles sont diffusées publiquement ; le secret n'est pas l'objectif. Le réseau doit vérifier que le titulaire du compte a bien autorisé la transaction. Une signature numérique prouve que vous connaissez la clé privée $d$ sans la révéler, et lie cette preuve à un message spécifique. Pour signer un message $m$ avec la clé privée $d$ : $$s = k^{-1}(z + rd) \mod n$$ La signature est la paire $(r, s)$. Étant donné un message $m$, une signature $(r, s)$ et une clé publique $Q$ : Le vérificateur reconstruit $R$ sans connaître $k$ ou $d$. Voici le raisonnement : $$P = u_1 G + u_2 Q = zs^{-1}G + rs^{-1}Q$$ Puisque $Q = dG$ : $$P = zs^{-1}G + rs^{-1}dG = s^{-1}(z + rd)G$$ D'après l'équation de signature, $s = k^{-1}(z + rd)$, donc $s^{-1} = k/(z + rd)$. En substituant : $$P = \frac{k}{z + rd}(z + rd)G = kG = R$$ La coordonnée x de $P$ égale $r$ précisément quand le signataire connaissait $d$. La valeur aléatoire $k$ doit être vraiment aléatoire et jamais réutilisée. Si le même $k$ signe deux messages différents, un attaquant peut retrouver algébriquement votre clé privée $d$. Ce n'est pas théorique : la signature de code de la PlayStation 3 de Sony a été cassée en 2010 parce qu'ils utilisaient un $k$ constant, permettant aux attaquants d'extraire la clé privée et de signer du code arbitraire. Une courbe elliptique, un problème difficile, deux protocoles. ECDH assure la confidentialité : deux parties dérivent une clé partagée sur un canal public, puis l'utilisent pour le chiffrement symétrique. ECDSA assure l'authenticité : prouver que vous avez autorisé quelque chose sans révéler votre clé privée. Cela montre comment la théorie abstraite des groupes de la 1re partie n'est pas seulement des mathématiques élégantes. C'est le fondement qui sécurise vos messages chiffrés, vos transactions de cryptomonnaie et une grande partie de l'infrastructure d'Internet. Ce billet a été écrit en collaboration avec Claude (Opus 4.5).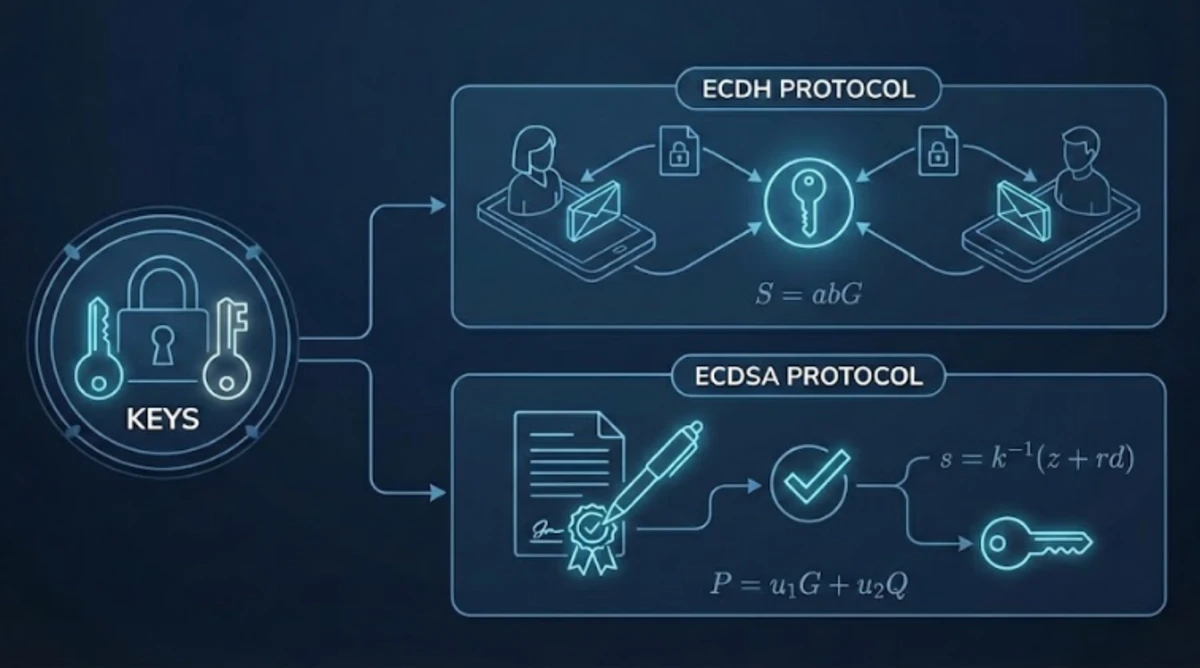
ECDH : Clés partagées
Le problème
Le protocole
ECDSA : Signatures numériques
Signature
Vérification
Pourquoi la vérification fonctionne
Le nonce
À retenir