KVキャッシュの無効化
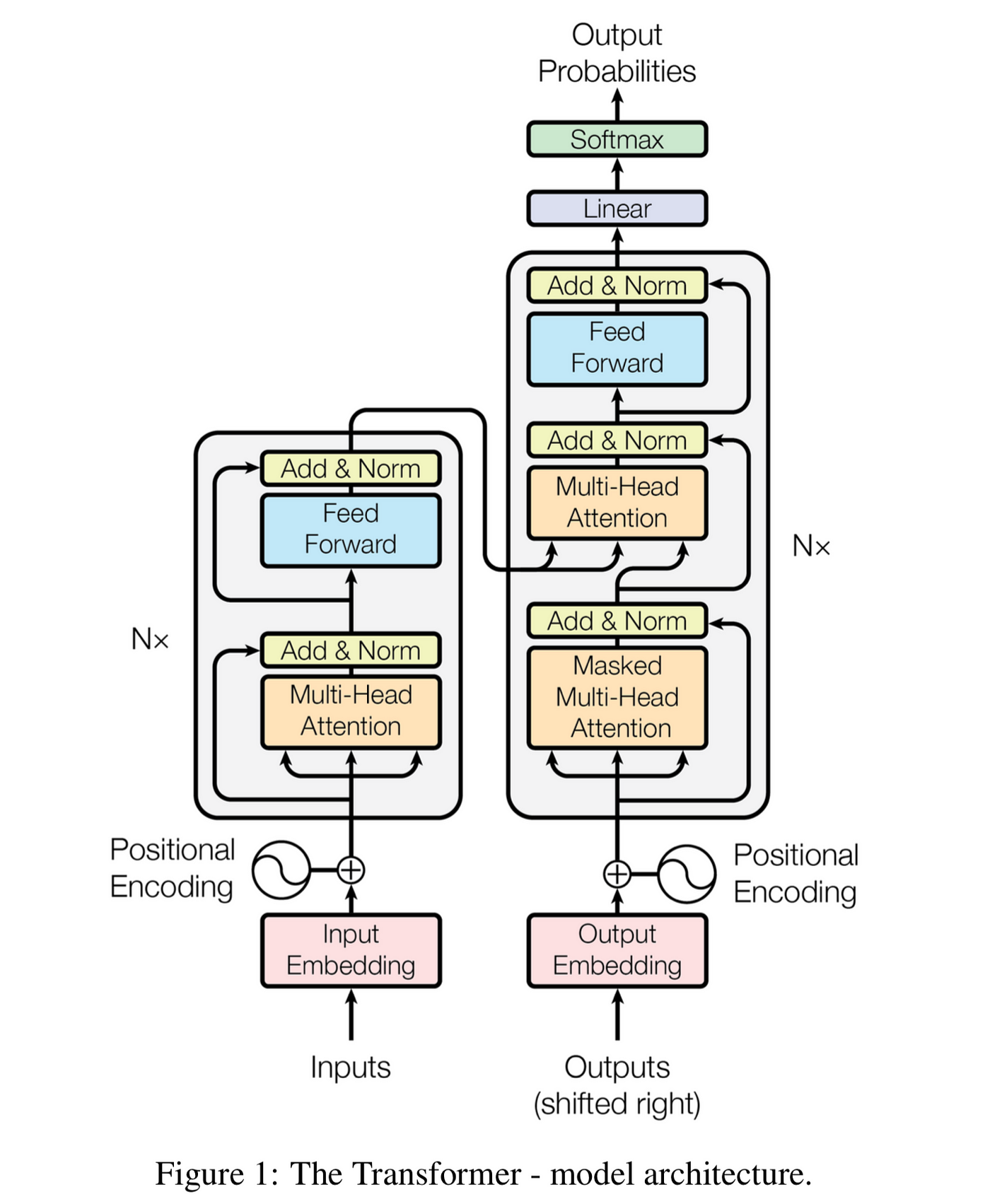
LLMの会話からコンテキストを削除すると完全な再計算が必要になる理由 年末年始の休暇中、友人とプロンプトキャッシングについて話をした。コンテキストエンジニアリングに関しては、誰もが自然とこう考える:ChatGPTやClaudeとチャットしていて会話に無関係なコンテキストが溜まってきたら、それを削除すればモデルの焦点が絞られるはずだ。精度も上がるよね? 確かにそうだが、落とし穴がある。会話の途中からトークンを削除するとKVキャッシュが無効化される。KVキャッシュはLLM推論を高速化する重要なメカニズムだ。キャッシュされた計算を少し失うだけではない。編集以降のすべてを失うのだ。これがclaude.ai、ChatGPT、Claude Codeが以前のメッセージを頻繁に編集・削除しない理由だ1。Claude CodeのPMが述べているように:「コーディングエージェントは、ターン間でプロンプトキャッシュを維持しなければ採算が合わない。」この記事ではその理由を説明する。 コンパクション(圧縮)は行われるが、頻繁ではない。 LLMはテキストを一度に1トークンずつ生成する。トークン列 $t_1, \ldots, t_i$ が与えられると、モデルは次のトークンの確率分布を予測する: $$P(t_{i+1} | t_1, \ldots, t_i)$$ 応答を生成するには、モデルはこの分布からサンプリングし(上の図ではおそらくParis)、新しいトークンをコンテキストに追加して繰り返す。新しいトークンごとにモデル全体を通したフォワードパスが必要で、完全なコンテキストを処理する。 現代のLLMはトランスフォーマーアーキテクチャを使用している。以下は「Attention Is All You Need」の有名な図だ: 右側の「Nx」とマークされた灰色のボックスはデコーダブロックで、$L$ 回繰り返される。各ブロックにはマスク付きマルチヘッドアテンションとフィードフォワードネットワークが含まれている。2 各トークン $t_i$ は埋め込みベクトル $x_i$ として始まる。ブロックを通過するにつれて、このベクトルは変換される。ブロック $\ell$ を通過した後の位置 $i$ のベクトルを隠れ状態 $z_i^{(\ell)}$ と呼ぶ。 各ブロックは次のブロックに入力を渡す:$z_i^{(\ell)}$ は $z_i^{(\ell+1)}$ を計算するための入力となる。$L$ ブロックの後、最終的な隠れ状態 $z_i^{(L)}$ は $P(t_{i+1} | t_1, \ldots, t_i)$、つまり最初に示した確率分布を予測するために使用される。 この図はオリジナルのエンコーダ・デコーダアーキテクチャを示している。GPTやClaudeのような現代のLLMはデコーダのみ:左側(エンコーダ)とエンコーダ出力に対するアテンションを行う中央の「Multi-Head Attention」を省略している。 各ブロックのマスク付きマルチヘッドアテンションは、各隠れ状態 $z_i^{(\ell)}$ から3つのベクトルを計算する。すべての位置 $i$、すべてのブロック $\ell$、すべてのアテンションヘッド $h$ について(Llama 3.1 405Bは126ブロックと128ヘッドを持つ): 位置 $i$ は、そのクエリをキーと比較し、バリューの重み付き和を取ることで、すべての位置 $j \leq i$ に注目する。つまり $z_i^{(\ell)}$ と Q、K、V は $t_i$ だけでなくすべての先行トークンに依存する。 KVキャッシュは重要な観察を活用する:新しいトークンを生成する際、以前の位置のKベクトルとVベクトルは変化しない。だからキャッシュする。新しいトークンごとに、そのQ、K、Vを計算し、キャッシュされたKとVをアテンションに再利用する。これにより、トークンあたり $O(n^2)$ の作業が $O(n)$ になる。 位置 $j$ のトークンを削除することを考えよう。キャッシュされたKベクトルとVベクトルはどうなるか? トークン $j$ を削除すると、すべての隠れ状態 $z_{j+1}^{(\ell)}, z_{j+2}^{(\ell)}, \ldots$ が変化する。それらはすべて位置 $j$ に注目していたが、もはや注目しなくなるからだ。前のセクションで述べたように、隠れ状態が変化するとKベクトルとVベクトルも変化する。位置 $j$ 以降のキャッシュ全体が古くなる。 プロンプトキャッシングには正確なプレフィックス一致が必要。 AnthropicやOpenAIなどのAPIプロバイダーはプロンプトのKV状態をキャッシュしている。新しいリクエストが以前のものと正確なプレフィックスを共有していれば、キャッシュを再利用できる。しかし、何かを変更すると(途中の1トークンでも)、その時点以降のキャッシュは使えなくなる。 キャッシュ無効化は高コスト。 50,000トークンの会話の早い段階でトークンを編集することを考えよう。編集以降のすべての位置で、すべてのブロックとヘッドにわたってKベクトルとVベクトルを再計算する必要がある。Llama 3.1 405Bの場合、8億回以上のベクトル計算になる。Anthropicのプロンプトキャッシングでは、キャッシュヒットは基本入力トークンコストの10%で価格設定されている。キャッシュミスは全額を支払うことを意味する。レイテンシも影響を受ける:長いプロンプトの場合、キャッシュヒットは最初のトークンまでの時間を最大85%削減できる。 追加はできるが編集はできない。 末尾にトークンを追加するのは安い:キャッシュを拡張するだけだ。途中に挿入または削除すると、それ以降すべての再計算が強制される。これがチャットボットの会話履歴が増え続ける一方になりがちな理由だ。 精度とコストのトレードオフは現実のもの。 無関係なコンテキストを削除するとモデルの焦点が改善されるかもしれないが、計算コストを払うことになる。長い会話の場合、このコストは相当なものになりうる。それでも価値がある場合もあれば、そうでない場合も多い。一つのアプローチ:Lettaが提案しているのは、アイドル期間中に非同期でプロンプト編集を行う(「スリープタイムエージェント経由で」)ことで、ユーザーが待っていないときにキャッシュ再構築が行われるようにすることだ。 ここでの記法は上で使用したものと一致している。 $$x_i = E[t_i] + p_i, \quad E \in \mathbb{R}^{V \times d}, \quad p_i \in \mathbb{R}^d$$ ここで $t_i$ はトークンインデックス、$p_i$ は位置エンコーディングである。 $X^{(0)} = [x_1, \dots, x_n] \in \mathbb{R}^{d \times n}$ をトランスフォーマーブロックへの初期入力とする。 ブロック $\ell = 1, \dots, L$ について、入力 $X^{(\ell-1)} \in \mathbb{R}^{d \times n}$ に対して: マルチヘッドマスクアテンション ヘッド $h$ のクエリ、キー、バリュー: $$Q^{(h)}(x_i) = (W_h^{Q})^T x_i, \quad K^{(h)}(x_i) = (W_h^{K})^T x_i, \quad V^{(h)}(x_i) = (W_h^{V})^T x_i$$ ここで $W_h^{Q}, W_h^{K}, W_h^{V} \in \mathbb{R}^{d \times k}$。 マスク付きアテンション重み $$\alpha_{i,j}^{(h)} = softmax_j \left(\frac{Q^{(h)}(x_i) \cdot K^{(h)}(x_j)}{\sqrt{k}} + M_{i,j}\right)$$ ここで因果マスク $M_{i,j} = 0$($j \leq i$ の場合)、$M_{i,j} = -\infty$($j > i$ の場合)。 各ヘッドの出力 $$u_i^{(h)} = \sum_{j=1}^{i} \alpha_{i,j}^{(h)} V^{(h)}(x_j) \in \mathbb{R}^{k}$$ 連結出力 $$u_i' = \sum_{h=1}^{H} (W_h^{O})^T u_i^{(h)}, \quad W_h^{O} \in \mathbb{R}^{k \times d}$$ 残差 + LayerNorm $$u_i = \text{LayerNorm}(x_i + u_i'; \gamma_1, \beta_1)$$ 各位置 $i$ について: $$z_i' = (W_2)^T \text{ReLU}((W_1)^T u_i), \quad W_1 \in \mathbb{R}^{d \times m}, , W_2 \in \mathbb{R}^{m \times d}$$ 残差 + LayerNorm(ブロック出力) $$z_i = \text{LayerNorm}(u_i + z_i'; \gamma_2, \beta_2)$$ $X^{(\ell)} = [z_1, \dots, z_n]$ とする。これがブロック $\ell + 1$ への入力となる。 $L$ ブロックの後、$Z = X^{(L)}$ を最終表現とする。 $$\text{logits}_i = E z_i + b, \quad E \in \mathbb{R}^{V \times d}, , b \in \mathbb{R}^V$$ ここで $E$ はしばしば入力埋め込みと共有される。 予測確率 $$P(t_{i+1} | t_1, \dots, t_i) = \text{softmax}(\text{logits}_i)$$ 位置 $i$ の出力は次のトークン $t_{i+1}$ を予測し、因果マスクによりトークン $t_1, \dots, t_i$ からの情報のみを使用する。 参考文献: この記事はClaude(Opus 4.5)と協力して書きました。
次トークン予測
トランスフォーマーのフォワードパス
KVキャッシュ
トークンを削除するとキャッシュが壊れる理由
実際の影響
付録:トランスフォーマーの数学
完全な導出
記法
ステップ1:入力トークン埋め込み
ステップ2-6:デコーダブロック(L回繰り返し)
ステップ7-8:フィードフォワードネットワーク
ステップ9-10:出力ロジットと確率