鍵からプロトコルへ:ECDHとECDSA(第2回/全2回)
楕円曲線の数学が安全な鍵交換とデジタル署名をどう可能にするか 第1回では、必要な道具を組み立てた。体、群、楕円曲線、そして離散対数問題(DLP)だ。鍵ペアで締めくくった。秘密の整数を選び(あちらでは $n$ と呼んだが、標準的な暗号表記に合わせてここでは $d$ を使う)、次を計算する。 $$Q = dG$$ $Q$ が公開鍵、$d$ が秘密鍵だ。順方向は高速だが、$Q$ から $d$ を復元するにはDLPを解く必要があり、これは実行不可能だ。 この記事では、この非対称性が異なる問題を解決する2つのプロトコルをどう可能にするかを示す。共有鍵を確立するためのECDHと、デジタル署名のためのECDSAだ。 AliceはBobに秘密のメッセージを送りたい。暗号化はメッセージを暗号文に変換し、復号はその逆を行う。 共通鍵暗号は両方の操作に1つの鍵を使う。高速だが、ブートストラップ問題がある。Aliceはどうやってその鍵をBobに送るのか。メッセージと同じチャネルで送れば、盗聴者が両方を傍受する。鍵を送るための安全なチャネルが必要だが、それはまさに作ろうとしているものだ。鶏と卵。 公開鍵暗号はこれを解決できる。誰でもBobの公開鍵で暗号化できるが、Bobの秘密鍵だけが復号できる。秘密がネットワーク上を流れない。代償は?公開鍵の操作には計算コストの高い演算(点の乗算、モジュラー累乗)が必要だが、共通鍵暗号は単純なビット演算を使う。複雑さの差は約1000倍だ。 解決策はハイブリッドアプローチだ。公開鍵暗号を1回使って共有鍵を確立し、実際のメッセージには共通鍵に切り替える。これがまさにECDHの役割だ。 楕円曲線ディフィー・ヘルマン鍵共有は、2者が公開チャネル上で共有鍵を導出できるようにする。 両者は $a$ も $b$ も送信せずに同じ点 $S$ に到達する。なぜ機能するのか。$a(bG) = (ab)G = b(aG)$ だからだ。この可換性は曲線の特別な性質ではなく、整数の乗法に由来する。 なぜ安全なのか。盗聴者は $A$、$B$、$G$ を見るが、これらから $abG$ を計算するには $a$ か $b$ を復元するためにDLPを解く必要がある。それは第1回で確立した困難な方向だ。 その後の流れ:AliceとBobは $S$ のx座標をハッシュして共通鍵を導出し、AES(共通鍵暗号の標準規格)のような暗号方式でそれを使う。ECDH自体は何も暗号化しない。共通鍵暗号を可能にする共有鍵をブートストラップするだけだ。1 最近の鍵でPGPやGPGを使ったことがあれば、これを使っている。ハイブリッド構造は同じだ。ECDHがセッション鍵を確立し、AESがメッセージを暗号化する。 2者間ではうまく機能する。グループチャットはより難しい。単純なアプローチでは $N$ 人の参加者に対して $\binom{N}{2} = \frac{N(N-1)}{2}$ 回の一対一の鍵交換が必要になる。実際のメッセージングアプリは、この二次関数的な増加を避けるためにより洗練されたプロトコルを使っている。 ECDHは機密性を解決する。ECDSA(楕円曲線DSA)は別の問題、すなわち真正性を解決する。 Ethereumのトランザクションを考えよう。公開でブロードキャストされる。機密性が目的ではない。ネットワークはアカウント所有者が実際にトランザクションを承認したことを検証する必要がある。デジタル署名は秘密鍵 $d$ を知っていることを明かさずに証明し、その証明を特定のメッセージに紐づける。 秘密鍵 $d$ でメッセージ $m$ に署名するには、 $$s = k^{-1}(z + rd) \mod n$$ 署名はペア $(r, s)$ だ。 メッセージ $m$、署名 $(r, s)$、公開鍵 $Q$ が与えられたとき、 検証者は $k$ も $d$ も知らずに $R$ を再構成する。その代数的な仕組みは以下の通りだ。 $$P = u_1 G + u_2 Q = zs^{-1}G + rs^{-1}Q$$ $Q = dG$ なので、 $$P = zs^{-1}G + rs^{-1}dG = s^{-1}(z + rd)G$$ 署名の式より $s = k^{-1}(z + rd)$ なので、$s^{-1} = k/(z + rd)$。代入すると、 $$P = \frac{k}{z + rd}(z + rd)G = kG = R$$ $P$ のx座標が $r$ に等しいのは、まさに署名者が $d$ を知っていたときだ。 ランダム値 $k$ は真にランダムで、決して再利用してはならない。同じ $k$ で2つの異なるメッセージに署名すると、攻撃者は代数的に秘密鍵 $d$ を復元できる。これは理論上の話ではない。ソニーのPlayStation 3のコード署名は、定数 $k$ を使っていたため2010年に破られた。攻撃者は秘密鍵を抽出し、任意のコードに署名できるようになった。 1つの楕円曲線、1つの困難な問題、2つのプロトコル。 ECDHは機密性をもたらす。2者が公開チャネル上で共有鍵を導出し、それを共通鍵暗号に使う。ECDSAは真正性をもたらす。秘密鍵を明かさずに、何かを承認したことを証明できる。 これは第1回の抽象的な群論が単なるエレガントな数学ではないことを示している。暗号化されたメッセージ、暗号通貨のトランザクション、そしてインターネットのインフラの多くを守る基盤なのだ。 この記事はClaude(Opus 4.5)と協力して書きました。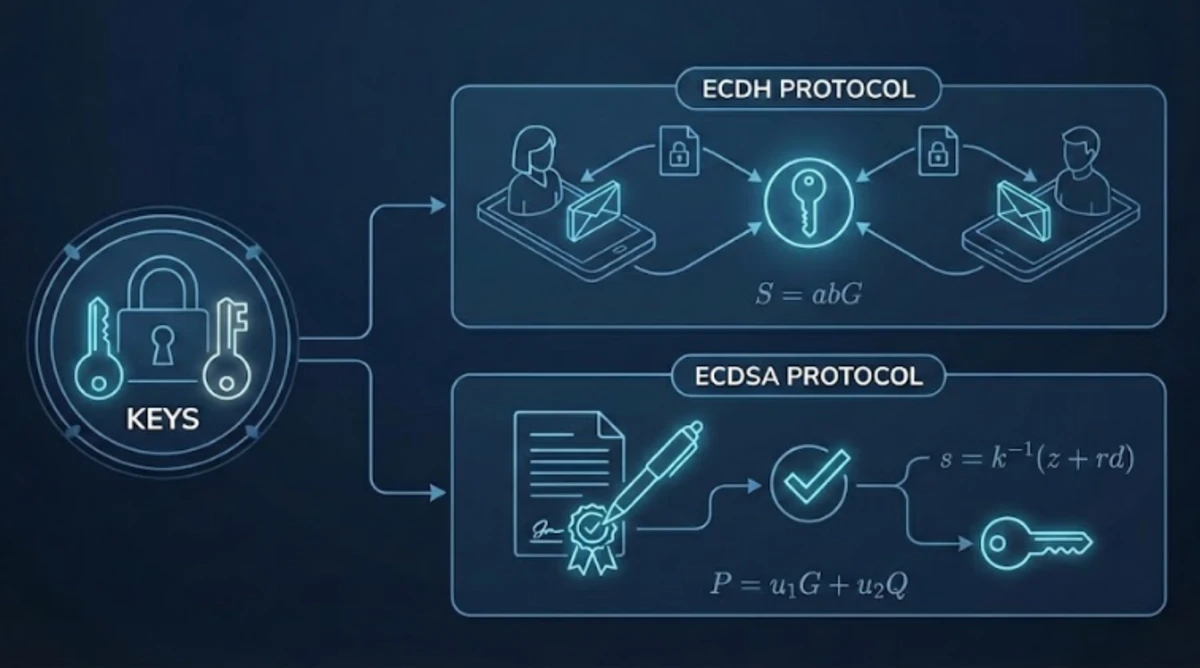
ECDH:共有鍵
問題
プロトコル
ECDSA:デジタル署名
署名
検証
なぜ検証が機能するのか
ノンス
まとめ